Since the accumulated PageRank of all pages of the web equals the total number of web pages, it follows directly that an additional web page increases the added up PageRank for all pages of the web by one. But far more interesting than the effect on the added up PageRank of the web is the impact of additional pages on the PageRank of actual websites.
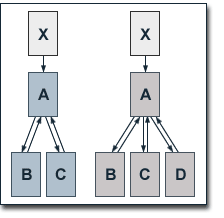
To illustrate the effects of addional web pages, we take a look at a hierachically structured web site consisting of three pages A, B and C, which are joined by an additional page D on the hierarchically lower level of the site. The site has no outbound links. A link from page X which has no other outbound links and a PageRank of 10 points to page A. At a damping factor d of 0.75, the equations for the single pages' PageRank values before adding page D are given by
PR(A) = 0.25 + 0.75 (10 + PR(B) + PR(C))
PR(B) = PR(C) = 0.25 + 0.75 (PR(A) / 2)
PR(B) = PR(C) = 0.25 + 0.75 (PR(A) / 2)
Solving the equations gives us the follwing PageRank values:
PR(A) = 260/14
PR(B) = 101/14
PR(C) = 101/14
PR(B) = 101/14
PR(C) = 101/14
After adding page D, the equations for the pages' PageRank values are given by
PR(A) = 0.25 + 0.75 (10 + PR(B) + PR(C) + PR(D))
PR(B) = PR(C) = PR(D) = 0.25 + 0.75 (PR(A) / 3)
PR(B) = PR(C) = PR(D) = 0.25 + 0.75 (PR(A) / 3)
Solving these equations gives us the follwing PageRank values:
PR(A) = 266/14
PR(B) = 70/14
PR(C) = 70/14
PR(D) = 70/14
PR(B) = 70/14
PR(C) = 70/14
PR(D) = 70/14
As to be expected since our example site has no outbound links, after adding page D, the accumulated PageRank of all pages increases by one from 33 to 34. Further, the PageRank of page A rises marginally. In contrast, the PageRank of pages B and C depletes substantially.
The Reduction of PageRank by Additional Pages
By adding pages to a hierarchically structured websites, the consequences for the already existing pages are nonuniform. The consequences for websites with a different structure shall be shown by another example.
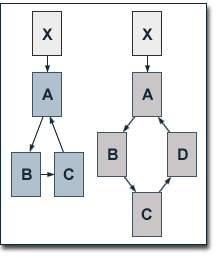
We take a look at a website constisting of three pages A, B and C which are linked to each other in circle. The pages are then joined by page D which fits into the circular linking structure. The regarded site has no outbound links. Again, a link from page X which has no other outbound links and a PageRank of 10 points to page A. At a damping factor d of 0.75, the equations for the single pages' PageRank values before adding page D are given by
PR(A) = 0.25 + 0.75 (10 + PR(C))
PR(B) = 0.25 + 0.75 × PR(A)
PR(C) = 0.25 + 0.75 × PR(B)
PR(B) = 0.25 + 0.75 × PR(A)
PR(C) = 0.25 + 0.75 × PR(B)
Solving the equations gives us the follwing PageRank values:
PR(A) = 517/37 = 13.97
PR(B) = 397/37 = 10.73
PR(C) = 307/37 = 8.30
PR(B) = 397/37 = 10.73
PR(C) = 307/37 = 8.30
After adding page D, the equations for the pages' PageRank values are given by
PR(A) = 0.25 + 0.75 (10 + PR(D))
PR(B) = 0.25 + 0.75 × PR(A)
PR(C) = 0.25 + 0.75 × PR(B)
PR(D) = 0.25 + 0.75 × PR(C)
PR(B) = 0.25 + 0.75 × PR(A)
PR(C) = 0.25 + 0.75 × PR(B)
PR(D) = 0.25 + 0.75 × PR(C)
Solving these equations gives us the follwing PageRank values:
PR(A) = 419/35 = 11.97
PR(B) = 323/35 = 9.23
PR(C) = 251/35 = 7.17
PR(D) = 197/35 = 5.63
PR(B) = 323/35 = 9.23
PR(C) = 251/35 = 7.17
PR(D) = 197/35 = 5.63
Again, after adding page D, the accumulated PageRank of all pages increases by one from 33 to 34. But now, any of the pages which already existed before page D was added lose PageRank. The more uniform PageRank is distributed by the links within a site, the more likely will this effect occur.
Since adding pages to a site often reduces PageRank for already existing pages, it becomes obvious that the PageRank algorithm tends to privilege smaller web sites. Indeed, bigger web sites can counterbalance this effect by being more attractive for other webmasters to link to them, simply because they have more content.
None the less, it is also possible to increase the PageRank of existing pages by additional pages. Therefore, it has to be considered that as few PageRank as possible is distributed to these additional pages.

No comments:
Post a Comment